Mplus is a statistical modeling program that provides researchers with a flexible tool to analyze their data. Mplus offers researchers a wide choice of models, estimators, and algorithms in a program that has an easy-to-use interface and graphical displays of data and analysis results. Mplus allows the analysis of both cross-sectional and longitudinal data, single-level and multilevel data, data that come from different populations with either observed or unobserved heterogeneity, and data that contain missing values. Analyses can be carried out for observed variables that are continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types. In addition, Mplus has extensive capabilities for Monte Carlo simulation studies, where data can be generated and analyzed according to any of the models included in the program.

The Mplus modeling framework draws on the unifying theme of latent variables. The generality of the Mplus modeling framework comes from the unique use of both continuous and categorical latent variables. Continuous latent variables are used to represent factors corresponding to unobserved constructs, random effects corresponding to individual differences in development, random effects corresponding to variation in coefficients across groups in hierarchical data, frailties corresponding to unobserved heterogeneity in survival time, liabilities corresponding to genetic susceptibility to disease, and latent response variable values corresponding to missing data. Categorical latent variables are used to represent latent classes corresponding to homogeneous groups of individuals, latent trajectory classes corresponding to types of development in unobserved populations, mixture components corresponding to finite mixtures of unobserved populations, and latent response variable categories corresponding to missing data.

The Mplus Modeling Framework

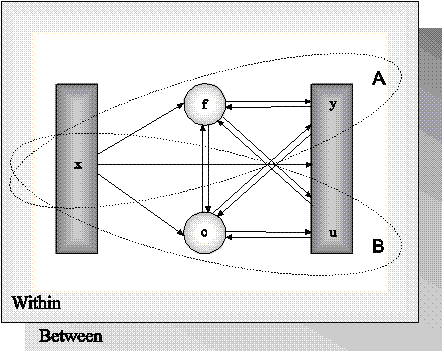
The purpose of modeling data is to describe the structure of data in a simple way so that it is understandable and interpretable. Essentially, the modeling of data amounts to specifying a set of relationships between variables. The figure below shows the types of relationships that can be modeled in Mplus. The rectangles represent observed variables. Observed variables can be outcome variables or background variables. Background variables are referred to as x; continuous and censored outcome variables are referred to as y; and binary, ordered categorical (ordinal), unordered categorical (nominal), and count outcome variables are referred to as u. The circles represent latent variables. Both continuous and categorical latent variables are allowed. Continuous latent variables are referred to as f. Categorical latent variables are referred to as c.

The arrows in the figure represent regression relationships between variables. Regressions relationships that are allowed but not specifically shown in the figure include regressions among observed outcome variables, among continuous latent variables, and among categorical latent variables. For continuous outcome variables, linear regression models are used. For censored outcome variables, censored (tobit) regression models are used, with or without inflation at the censoring point. For binary and ordered categorical outcomes, probit or logistic regressions models are used. For unordered categorical outcomes, multinomial logistic regression models are used. For count outcomes, Poisson and negative binomial regression models are used, with or without inflation at the zero point.